Lorenz (Poincaré) Return Map
A Lorenz return map (also called a Poincaré first return map or plot) is a sophisticated mathematical tool for investigating dynamical systems. However, a useful application in neuroscience has a surprisingly simple implementation, and just involves plotting the value of an item in a sequence, against the value of the next item in the sequence. Typically, each item could be the peak (or trough) value of successive cycles in an oscillating system. Lorenz plots of this sort can reveal “meta”-rhythms, i.e. rhythms within rhythms, like the beat frequency of mixed oscillators, and is used in investigating biological phenomena such as heart beat and respiratory or locomotory rhythms.
- Load file Lorenz plot sin40.
This shows a noisy sine wave with a 25 ms cycle period. Two regular point process event trains have been generated with the sine wave as their parent trace: a has a 10 ms interval, while b has a 9 ms interval. This means that event channel a will return to the same data value in its parent trace every 5th event (50 ms), while channel b will only return every 25th event (225 ms). So for channel a, there will be 5 different values of Vn/Vn+1, while for channel b there will be 25 such values. However, because the sine wave is noisy, the values will form clusters, rather than exactly-superimposing points.
- Select the Event analyse: Lorenz (Poincaré) return plot menu command to display the Lorenz (Poincaré) Return Plot dialog.
By default the plot shows the average data values within the events, although other parameters can be selected from the drop-down Parameter list. With the default channel a selected as the source event, the 5 clusters representing the 5 different values of Vn/Vn+1 are obvious in the display.
- Select event channel b.
- Check the Colour time box.
This colours the points in the plot according to the time in the data file at which event n occurs.
The plot now forms a ring structure, reflecting the more complex relationship between successive values of a metarhythm which repeats every 25 cycles of the base rhythm. The plot should look like the image below.
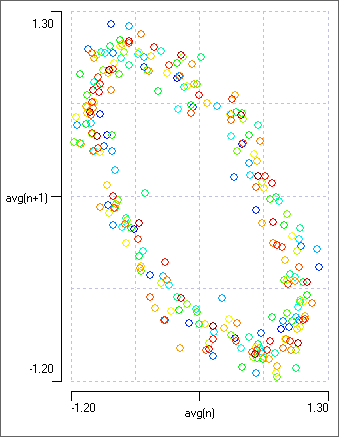
Lorenz plots are also commonly used to investigate frequency distributions, in which case the frequency or interval parameter should be selected.